信号処理の概要と数理的アプローチの意味

適応信号処理と非線形への拡張

2022年2月、第18回日本学術振興会賞を受賞しました。
受賞理由：モデル選択に基づく非線形推定による革新的適応信号処理分野の開拓

授賞式はcovid19の感染拡大によって中止となりましたが、2024年3月に秋篠宮皇嗣同妃両殿下のご臨席の下、明治記念館で挙行された「第20回日本学術振興会賞並びに日本学士院学術奨励賞」授賞式と記念茶会に来賓として出席してきました。以下、受賞理由となった一連の研究内容について、理工系の大学生くらいを想定して説明してみたいと思いますので、ご一読いただければ幸いです。

線形モデルと適応信号処理

湯川（本研究室の主宰者）は，新世代情報通信システムを実現するための新しい適応信号処理パラダイムを構築することを目的として研究を続けてきました．
「信号処理の概要と数理的アプローチの意義」の問題設定で，関数fが時間変動する状況を考えます．
例えば，無線通信の通信路（携帯電話から基地局への経路）を考えてみると，携帯電話を持った人が移動すれば通信路fが変化します．
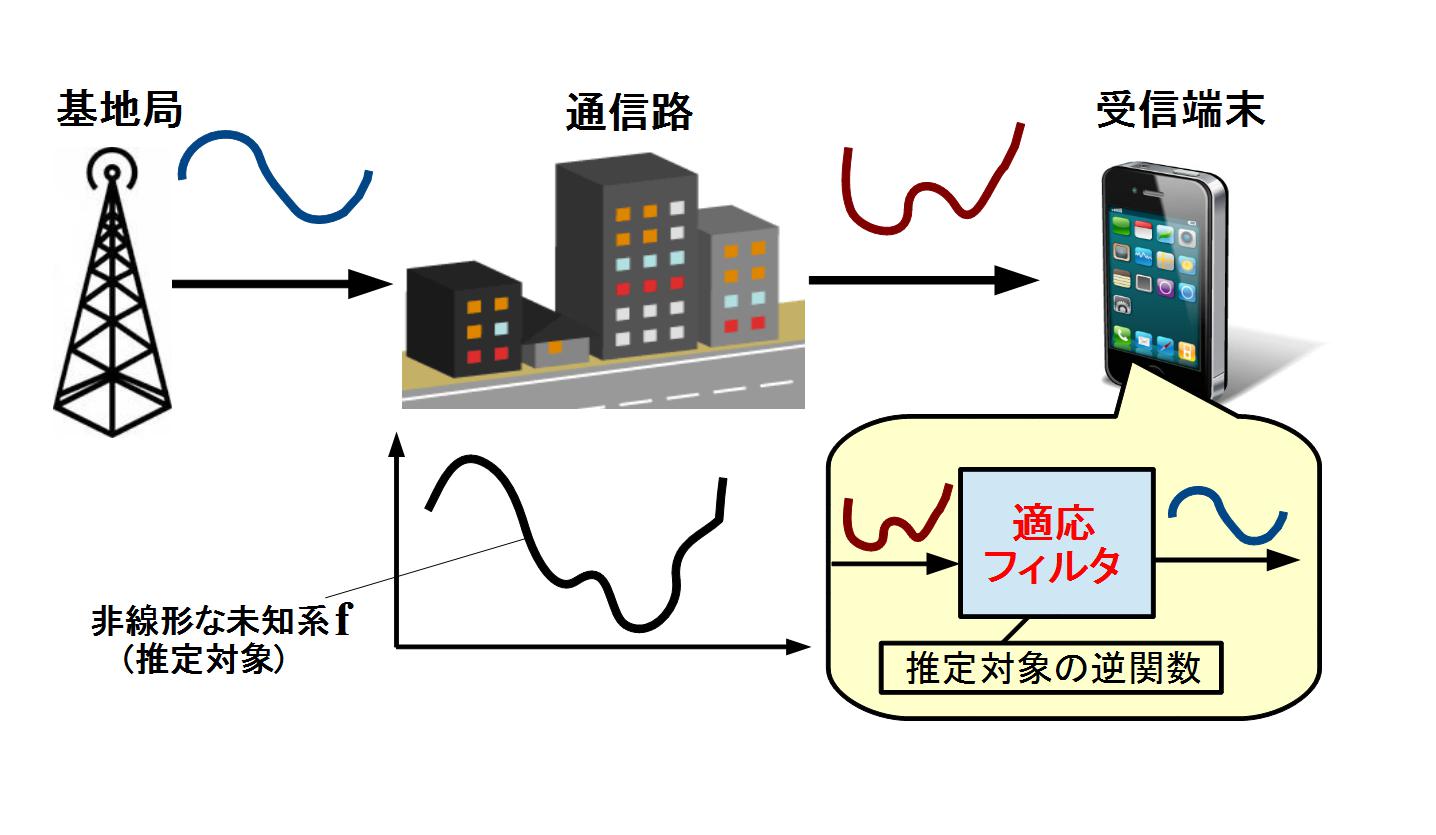
このような場合に関数fを適応的に追従していくのが適応信号処理です． kernel
適応信号処理では，(x_1,y_1), (x_2,y_2) ．．．の組が時間の経過とともに順次，観測されていきます．
それぞれの信号yは，各時刻の関数fによって，y=f(x)で与えられます．
順次，観測される情報を基に，関数fの逆関数を探していきます．

ここで一つポイントとなるのは，関数fの逆関数をどのようにモデル化するかということです．
数理モデルの選択は，数理科学全般における中心的課題ですが，もっとも基本的で，かつ汎用性の高いモデルが線形モデルです．
大雑把に言えば，xとyが比例関係にあるようなモデルです．
このとき，観測信号をサンプリングして得られるベクトルをyとすると，xはyと「あるベクトルh」の内積（ベクトルyとhの成分毎の積和）で表現できます．
ベクトルhのことを線形フィルタと呼びます．観測信号yをフィルタhに通すことで，欲しい特定の情報xを抽出するというイメージを持つと，フィルタという表現がしっくりきます．
珈琲をイメージするともっと良いでしょう．

適応フィルタとその課題

順次，観測されるxとyを手掛かりとして，あるルールにしたがって線形フィルタhを更新していき，時間変化する関数fの逆関数を推定・追従していきます．
これを適応フィルタと呼び，フィルタを更新するルールを適応アルゴリズムと呼びます．
適応アルゴリズムには長い歴史がありますが，アルゴリズムに要請される以下３つの性質の間にはトレードオフがあり，これを解消することが望まれていました．
(a) 収束速度が速い → 短い時間（少ない観測信号）で最適な線形フィルタの良い推定が得られる．
(b) 計算量が少ない → 実時間処理が可能，低消費電力（電池の寿命やグリーンイノベーションに直結）．
(c) 雑音・外乱・入力信号の統計的性質の変化などに対して頑健（ロバスト）である．
適応アルゴリズムの代表例であるLMS（Least Mean Square）アルゴリズムとRLS（Recursive Least Squares）アルゴリズムがこのトレードオフでいうと対局に位置します．
LMSは確率的勾配法と呼ばれることもあり，比較的単純なアルゴリズムであるため，計算量が少なく，雑音などに対して頑健である反面，音声信号のように相関の強い信号に対して収束速度が遅いという欠点があります．
一方，RLSは相関の強い信号に対しても高速な収束特性を持ちますが，計算量が多く，また，外乱や入力信号の統計的性質の変化の影響を受けやすいという欠点があります．
これらのアルゴリズムのそれぞれの欠点を補うために，無数の適応アルゴリズムが提案されてきましたが，トレードオフ問題を解消するアイディアはありませんでした．
湯川は，大学院で行なった適応信号処理研究の経験から，計算量やロバスト性を犠牲にすることなく高速な収束を実現するためには，何らかの「補足的な情報」を効果的に適応アルゴリズムに取り込むための数理的枠組みが不可欠であると考えました．
一言で言えば，「凸性を巧く利用した先験情報の活用法」が鍵であると確信したのです．
凸性は，大域的最適性と収束を保証し，強靭な理論体系を構築するために不可欠な性質です．
線形理論だけでは歯が立たないことは，LMSやRLSなどの例からも明白です．
そのために，凸解析（非線形解析）の知見が大きな助けとなります．
「補足的な情報」を効果的に利用するためのアイディアを提案してきました．
その中のほんの一部を「過去の研究テーマと今後」のページでも紹介していますが，いずれも「非拡大写像の不動点理論」が数理的基盤となっています．
だいぶ説明を省略しましたが，以上が2010年頃までのメインテーマと成果です．
これらの成果は学界・産業界の各方面から高く評価していただき，複数の賞を受賞することができました．下記文献で詳しく説明していますので、興味があれば、是非、手に取って読んでみてください。入門的な内容は、同連載講座の第一回・第二回で扱っています。

湯川正裕，第三回：不動点近似型適応アルゴリズムと応用, 日本音響学会誌, 連載講座：非線形適応信号処理への凸解析的アプローチ, 78巻 10号, pp.606--614, 2022. [ 無料公開]

再生核適応フィルタとモデル選択

2010年を境に，非線形への拡張を考え始めました．話はもう一度，数理モデルの選択に戻ります．
これまでの話は，関数fの逆関数が線形関数で十分良く近似できるケースを考えていました．
しかし，新世代情報通信システムとして応用を多方面へ広げていくためには，線形モデルでは良好に近似できないケースが出てきます．
例えば，脳波の例や金融データの予測，光通信路の推定など，挙げればキリがありません．
この場合，適切な数理モデルが一般には分からないので，「数理モデルの選択」と「選択されたモデルに基づく関数推定」という２つのタスクが生じます．
この２つのタスクを同時に自動化する新しい適応信号処理パラダイムを世界に先駆けて提案しました．
この新パラダイム「多カーネル適応フィルタ」は，再生核の理論，スパース最適化理論，不動点理論の知見を有機的につなげることで構築されています．
この研究成果は，米学術誌 IEEE Transactions on Signal Processing 2012年9月号などに掲載されています．
多カーネル適応フィルタは，今世紀になってから研究されるようになった再生核適応フィルタ（非線形適応フィルタの一種）をベースにしています．

まずは，再生核適応フィルタから説明しましょう．
再生核（reproducing kernels）は，関数のベクトル空間（正確にはヒルベルト空間）を考えた時に，各関数phiの引数xを定めたときの関数値phi(x)を内積によって表現する数学的道具です．
20世紀初頭から研究され，20世紀半ばに再生核ヒルベルト空間の理論が完成されましたが，実際に使われるようになったのはそれほど古くありません．
これが一番最初に使われたのは，恐らくサポートベクターマシン（SVM）でしょう．
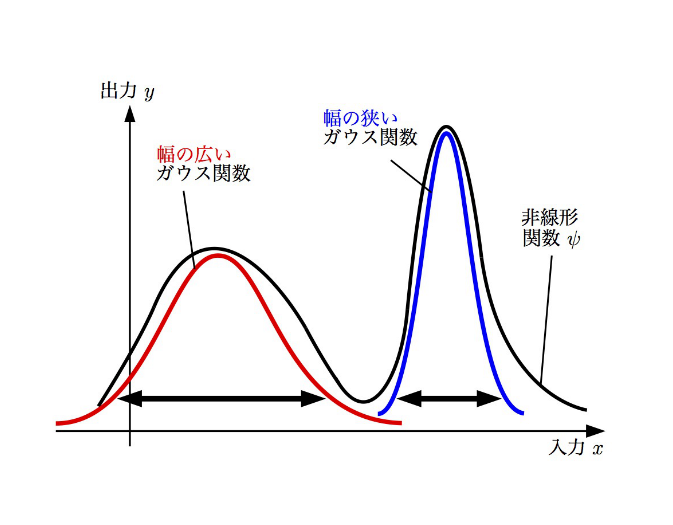
直感的には，ある幅を持つ面積１の山（例えば，ガウス関数）の和で非線形関数を表現すると思ってください． kernel

しかし，問題は，分からない非線形関数を推定するのに，どうやって適切な山の幅を決められるでしょうか．
言い換えれば，どうやって適切な数理モデルが選べるでしょうか．
幅が大き過ぎれば細かな変化は表現できないし，逆に小さ過ぎれば，ゆっくりとした変動を表わすのに，沢山の山を持ってこないと表現できないことになり，計算量やメモリの増大につながってしまいます．
また，雑音の影響も受けやすくなってしまいます．
つまり，ここにもトレードオフが生じることになり，数理モデル選択の自動化が切望されることになります．

多カーネル適応フィルタとモデル選択

多カーネル適応フィルタでは，予め，幅の小さい山から大きい山まで様々なものを用意しておきます．
そして，それぞれの山の高さを決める係数を巧く決めていきます．
そして，推定したい関数にフィットする山だけを使って表現したいので，フィットしない山の係数をゼロにします．
係数は行列で表現します．各列は各山に対応して，各行は山の位置に対応します．
ゼロを沢山含む行列のことをスパース行列（疎行列）と呼びます．
広い大地に疎らにしか草が生えていないような状況を思い浮かべると良いでしょう．
そのため，スパース最適化として問題を定式化します．
そして，それを効率的に解くために不動点理論の最新の知見が利用できることが明らかになります．
こうして，新しい非線形適応信号処理パラダイムが本研究室で産声をあげました．

それから10年以上の歳月が経ち、様々な研究成果が得られましたので、その一部を以下に掲載しておきます。特に、Fraunhofer HHI研究所との共同研究により、無線通信への応用において、著しい有用性が実証されました。その成果は、文献1,6や国際会議論文に加えて、未来の無線通信のための機械学習技術をまとめた研究書(wiley社より2020年出版)にも掲載されています。

Daniyal Amir Awan, Renato Luis Garrido Cavalcante, Masahiro Yukawa, and Slawomir Stanczak, "Adaptive Learning for Symbol Detection: A Reproducing Kernel Hilbert Space Approach," in Machine Learning for Future Wireless Communications, Chapter 11, Editor: Fa-Long Luo, pp.197--211, Wiley, 2020.

2022年には、日本音響学会誌への連載記事を執筆する機会にも恵まれ、一連の研究を紹介しています。

湯川正裕, 第五回(最終): 非線形適応フィルタと応用：再生核と不動点近似型アルゴリズムの出会い, 日本音響学会誌, 連載講座：非線形適応信号処理への凸解析的アプローチ, 78巻 12号, pp.730--739, 2022. [ 無料公開]

これらの研究を支えてくださった関係各位に、心より感謝申し上げます。

Top Researchers 時間変化する複雑な現象を読み解くための数学理論を構築する～湯川正裕・慶應義塾大学理工学部電気情報工学科教授

河合塾みらいぶっく, 信号処理激増する通信量・流動的な通信環境に対応できる通信技術に数学で挑む

適応信号処理と非線形への拡張

線形モデルと適応信号処理

適応フィルタとその課題

再生核適応フィルタとモデル選択

多カーネル適応フィルタとモデル選択

関連記事

関連する研究成果

戻る