信号処理の概要と数理的アプローチの意義
信号処理工学(Signal Processing)を中心とした数理工学を研究することで,情報通信を初めとする様々な分野を支える基盤となる数理的技法を創り出しています.
例を見た方がイメージが湧くでしょう.右図は,音声信号の例です.
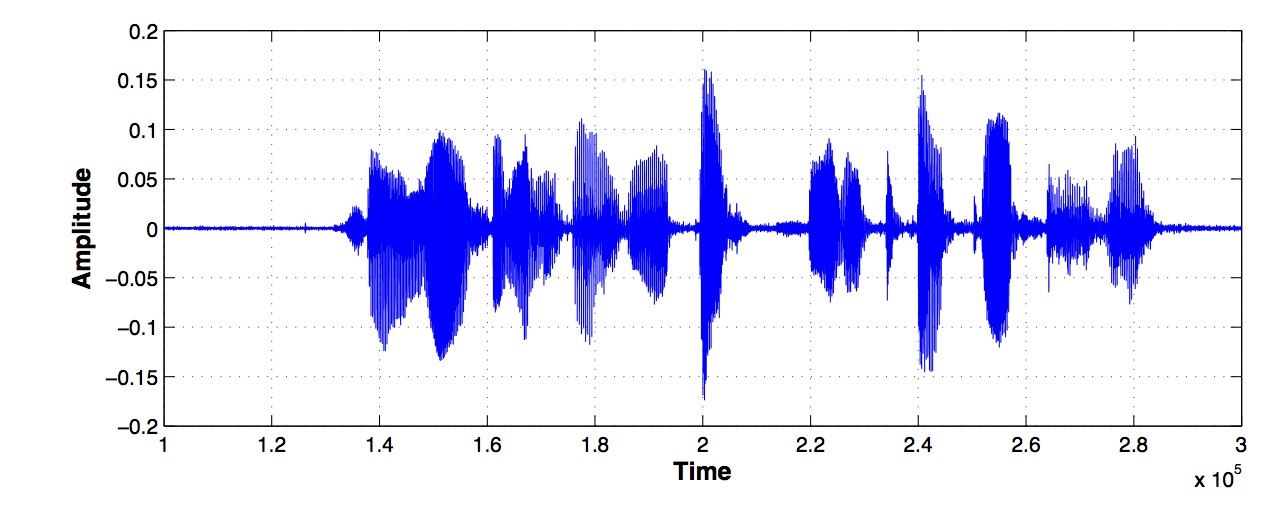
この他にも,画像,脳波,電波,地震波など,信号の種類は無数にあります.株価の変動などの金融データは,一見,信号と無関係に思えますが,これも信号処理の手法で解析できるので,ある種の信号として扱うことができます.
このように考えると,世の中の森羅万象に信号が潜んでいることに気がつきます.
信号は一般に数値で表現されます.金融データなどは明らかですが,音声,画像,脳波といった信号も,
それぞれマイクロホン,デジタルカメラ,脳波計に内蔵されたセンサーによってセンシングされて,
電気信号に変換されます.
この電気信号の電流の値が各信号の「数値」となるわけです.
数値化された信号は,(多くの場合,サンプリングの過程を経て)線形代数で主役を演じるベクトルや行列として表わされます.
信号処理分野は広範な内容を網羅しており,例えば,上で簡単に述べたセンシングやサンプリングも研究対象であり,現在でも様々な角度から進展が起こっています.
本研究室で主な研究対象としているのは,数値化された信号を如何にして扱うかというところです.
さて,いよいよ本題に入っていきます.
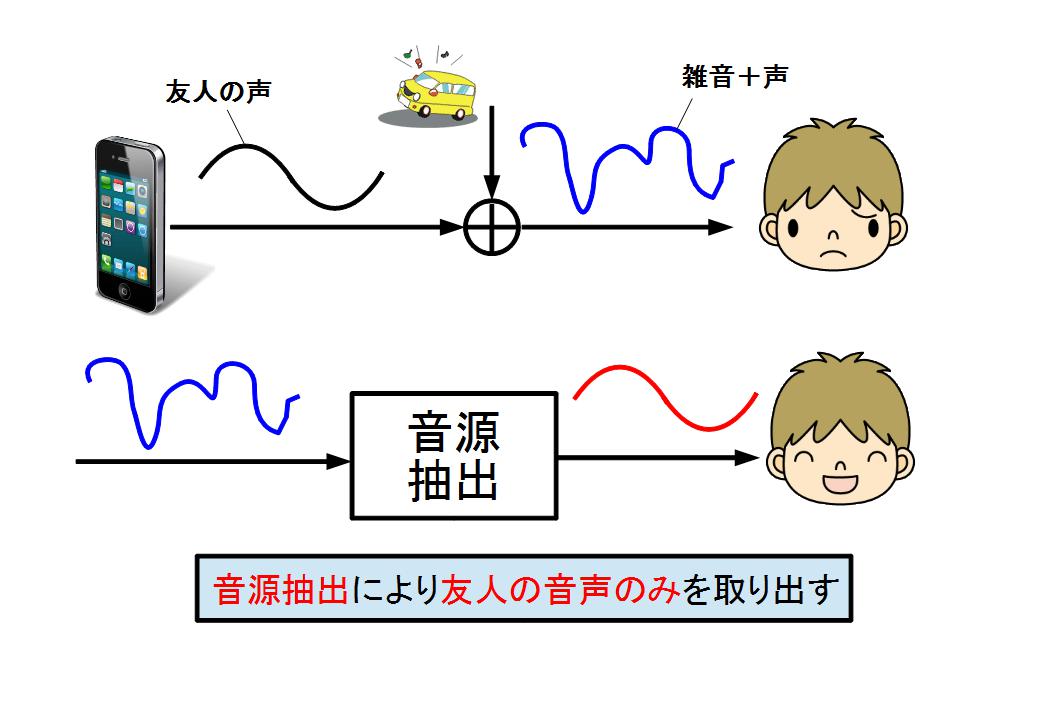
例えば,渋谷のスクランブル交差点を歩きながら,友達と携帯電話で会話しているとき,
携帯電話に搭載されたマイク(センサー)には,皆さんの話し声の他に様々な音が入ってきます.
皆さんの耳をセンサーと考えた場合には,友達の話し声の他に周囲の人の話し声や車のエンジン音,
夏であれば蝉の声などが聞こえているわけです.
しかし,皆さんはどんなにうるさい場所であっても,極端に言えば,演奏中の屋外ライブ会場にいたとしても
隣にいる友達の話し声を聞くことができるはずです.
勿論,演奏のボリュームと友達の声量の比(SN比と言います)
により,限界はあるわけですが...
専門的に言えば,複数の音源から発信された音声信号の和(混ざった音)から,特定の情報(友達の話し声)を
抽出していることになるわけです.
実は,これが信号処理でやろうとしていることの本質です.
この問題は信号処理分野で「音源分離」と呼ばれ,盛んに研究されています.
これに関連する本研究室の研究成果は「現在の研究テーマと今後について(研究テーマC)」で紹介します.
携帯電話に話しを戻すと,観測される信号は,欲しい情報(友達の話し声)の他に雑音(周囲の音)を含んでいるわけです.
どんな場所であろうと,エアコンの音,冷蔵庫の音,ボイラーの音など,自然界に存在する雑音から完全に逃れることは無理に近いでしょう.
画像の例では,焦点が合わずにぼけた画像が撮れてしまった場合や,記念写真を撮っているときに横切った歩行者がいた場合などを考えると,
私達が欲しい情報(ぼけてない画像,歩行者が写っていない画像)が得られない状況が多くあるわけです.
脳波の例では,波形の変化の様子から特定の情報(人が考えたこと)を取り出して,暮らしに役立てたいわけです.
地震波を利用して,地震発生の有無を予測したいでしょう.
上の例で見てきたように,私達は,様々な場面で信号から特定の情報を得たいと考えるわけですが,実際に観測される信号は,欲しい情報と一般に異なるわけです.
数学的に表現すると,分かりやすくなります.
欲しい特定の情報をxとしましょう.これは,友達の音声,ぼけてない画像,
人の意思(例えば,目の前にある食事を食べたければ1,そうでなければ0など),
地震発生の有無(1時間後に発生する確率が高ければ1,そうでなければ0など)に対応すると思ってください.
これに対して,観測される信号をyとします.
このとき,観測信号yがxに関する情報を全く含んでいなければ,yからxを当てる(推定する)ことはできません.
言い換えれば,yはxによって決まるもの,つまりyはxの関数であると考えるのが自然でしょう.
例えば,
y=f(x)
と書いた時,yからxを推定したいので,単純にいえば,fの逆関数を求めたいという問題になることが分かるでしょう.
観測される信号yは,欲しい情報xと関数fで決まる,別の言い方をすれば,yはfとxに関する「情報」を含んでいるという意味で
fを推定する手掛かりになりますが,多くの場合,yだけからfを高い精度で推定することはできません.
そこで,大抵は,答えが分かっているx_1, x_2, ..., x_n とそれぞれに対する観測データy_1, y_2,..., y_nを手掛かりに
関数fを推定して,答えが分からない観測データyからその正解xを推定します.
n個の食事を用意して,それを順番に見せて脳波(y_1, y_2,...,y_n)を測定し,食べたいと思ったかどうか(x_1,x_2,…,x_n)を記入してもらうことで,関数fを推定することで,
それ以外の食事が出てきたときの反応を脳波から推定できるようになるわけです.
上で述べた推定問題は,数理科学の分野では,特に逆問題と呼ばれます.
関数fによって姿を変えた信号yから,欲しい信号xを復元したいという言い方もできます.
どういった呼び方が適切かは応用によって異なりますが,数学的にはシンプルに定式化できることが分かります.
このように,信号復元,信号推定,データ予測,特徴抽出など,様々な名前で呼ばれる問題が,
数学的には共通の問題として取り扱うことができます.
応用によって,前提条件が異なったり,目的が異なったりするので細かく見れば違う問題と見ることもできるわけですが,
大きな視点から問題をみて,そこから個々の応用へ徐々に細分化していくような数理体系を築くことは人類の宝となります.
