過去の研究テーマ
研究テーマA
Nonlinear Adaptive Filtering Based on Kernels
(supported by KDDI Foundation)担当：外田脩・滝沢雅明
多カーネル適応フィルタに関連する研究テーマは，まだまだ山のようにあります．
本研究室では様々な方向への進展を目指して研究を続けています．
最近の成果は，国際会議「IEEE ICASSP2013；５月バンクーバー」で発表しました．
今後も，「EUSIPCO2013；9月マラケシュ」「AISIPA-ASC2013；10月台湾」などで発表予定です．
ベルリン工科大学・Fraunhofer HHI との共同研究を開始しました（2013.7.16 インターネット会議にて，研究の方向性を
議論しました．外田脩氏も参加）．
研究テーマB
Lp-Constrained Least Squares (0< p < 1) for Sparse Optimization
(supported by JSPS Grants-in-Aid)
担当：Jeong Kwangjin
スパース最適化は，信号処理・情報理論・統計・最適化などのコミュニティで盛んに研究されています．
その起源は幾つかあり，問題設定も様々ですが，一番分かりやすい基本的な定式化をここでは紹介しましょう．
x,y,zの3変数の１次方程式 ax + by + cz = d （a, b, c はゼロでない実数）の実数解が無限個あることは皆知っています．
大学で線形代数を学ぶと，左辺がベクトル(a,b,c)とベクトル（x,y,z）の内積になっていることが分かり，解集合を表現することが容易になります．
つまり，一つの解(x,y,z)=(d/a,0,0)に，(a,b,c)と直交するベクトルを足したベクトルも全て解であることが分かるわけです．
ベクトル(a,b,c)と直交するベクトル全体を考えると平面になりますので，解集合は平面になることがわかります．
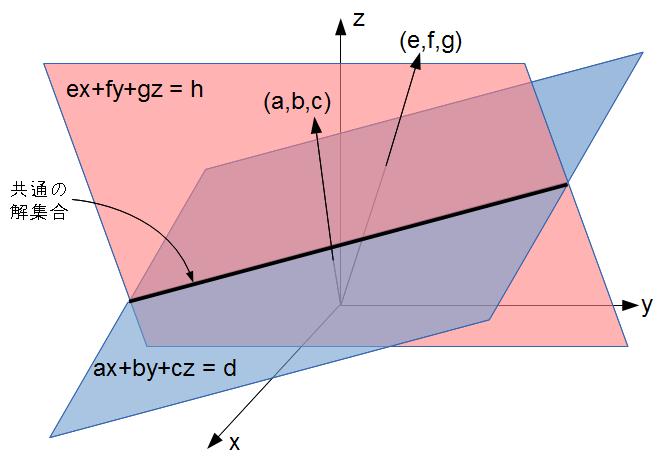
x,y,zの別の方程式 ex + fy + gz = h （e, f, g はゼロでない実数）が与えられれば，別の開集合（平面）ができます．
２つの平面が平行でなければ，つまり(a,b,c)が（e,f,g）の定数倍になっていなければ，２つの平面は交わり，共通部分は直線になります．
これが２つの連立１次方程式の解集合です．
そして，方程式の数が変数の数（ここでは変数はx,y,zなので3）に一致したとき，初めて解が一つに定まります．
以上は，線形代数のとても基本的な内容であって，これがn変数になっても話は変わらないことも容易に理解できます．
スパース最適化のルーツの一つである圧縮センシング（Compressed Sensing）は，欲しい情報（例えば，画像．
変数の数=画素数）が一つあるにも関わらず，観測できる情報（方程式の数）が不足しているために解集合までしか特定できない状況を考えます．
つまり，画像の候補が無限個得られるけど，どれが正解か分からない状況です．
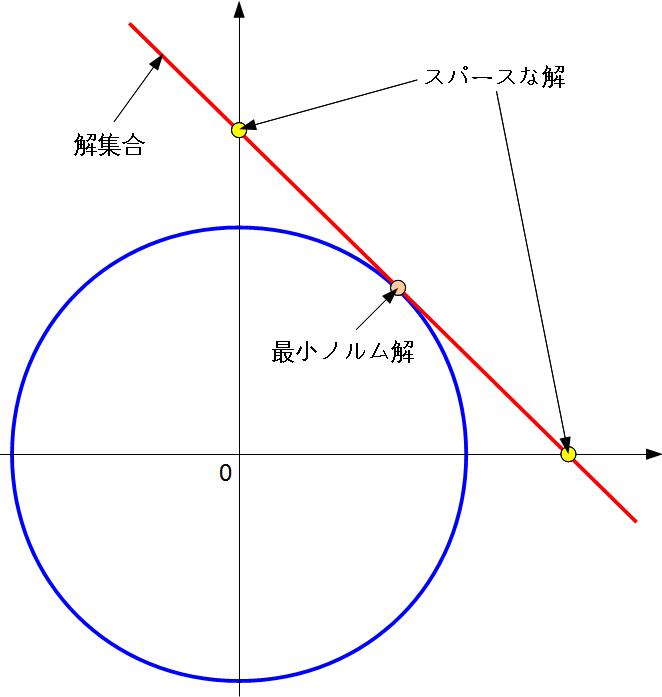
そもそも解を得るための情報が不足しているのだから，正解を求めることなんてできない，とりあえず原点に最も近い解（最小ノルム解）を採用しよう．
これが従来の妥協策で，一般化逆行列を用いることで計算できます．
しかし，「スパース性」を利用することで，情報が不足している状況でも正解を高い精度で得る方法が発見されたのです．
これは，同時に，長年，デジタル通信の原点である「シャノンの標本化定理」の前提条件である「帯域制限信号」という仮定をより現実的な仮定に置き換えることになります．
画像復元の例では，画像はウェーブレット基底で表現した場合にスパース表現できるという知見を使います．
つまり，画像そのものでなく，ウェーブレット基底の係数ベクトルを変数に置き直して，解集合の中から最もスパースなベクトルを求めることで正解が得られるのです．
スパースなベクトルを求める問題（スパース最適化問題）は組み合わせ最適化問題になって，画像のようにサイズの大きな問題を解こうとすると，NP困難であることが知られています．
しかし，ここで興味深い理論的な結果が示されました．
スパース最適化問題の解が，ある仮定の下で，ベクトルの各成分の絶対値和（L1ノルム）を最小化する解と高い確率で完全に一致するというものです．
本研究室では，L1最小化で巧く復元できない問題をLp準ノルム（0 < p < 1）を使って復元することを目指して研究しています．
Lp準ノルムは非凸関数であるため，様々な困難な問題が生じます．
そのために，L1ノルムの解をLagrange 未定乗数を用いて再定式化して，未定乗数を変化させたときの解の軌跡を求めるLARS（Least Angle Regression）という手法が提案されています．
湯川はこの手法をLp準ノルムの場合に拡張し，様々な非自明な知見が得られました．
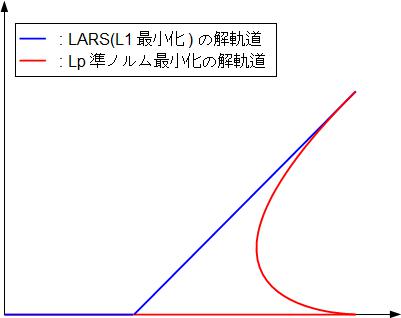その中の一つは，Lp準ノルム最小化の解（正確には臨界点）の軌跡がOrthogonal Matching Pursuit（OMP）というグリーディアルゴリズムと一致するというものです．
「ヒューリスティックなOMP」と「Lp最適化問題」の出会いは，大変興味深いことのように思われます．
この研究に関する初期成果は，情報理論の国際シンポジウム IEEE ISIT2012 （７月 MIT）で発表しました．
現在は，Jeong Kwangjin氏とともにこの研究を続けており，また一歩，進展が得られそうな状況です．
補足：研究テーマA, C, Dでは，L1最小化の原理を巧く利用しています．
研究テーマC
Supervised Nonnegative Matrix Factorization
(supported by SCAT Grants-in-Aid)
担当：森川優
Nonnegative matrix factorization (以下，NMF) は，信号処理の分野で盛んに研究されているデータ解析手法です．
解析対象となるデータは幅広く，音声・音楽，画像，脳信号，文書，行動履歴などがあります．
NMFは具体的にどのように使われるか，ということを音楽を例にして説明します．
音楽が持つ情報は様々ありますが，例えばメロディ，リズム，コード進行，楽式，ジャンル，使用される楽器などが挙げられる
と思います．
こういった情報を得ることが，音楽に対してNMFを適用した場合の目的にあたります．
本研究室では特に，音楽を自動的に楽譜化すること (自動採譜) を目指してNMFの研究をしています．
NMFの基本事項を簡単に説明します．
NMFにより得られる情報は，データを構成する「頻出パターン」です．
これは，音楽でいえば「ピアノのド」「ピアノのミ」などにあたります．
また，同時に，「頻出パターンがいつ現れるか」という情報も得られます．
そのため，音楽を解析すれば，「その音楽はどんな種類の音から構成されていて，各音がいつ鳴るか」ということが分かるわけです．
下図はピアノのドとミのみから構成された音楽 (楽器音) を，NMFによって解析したことを示す図です．
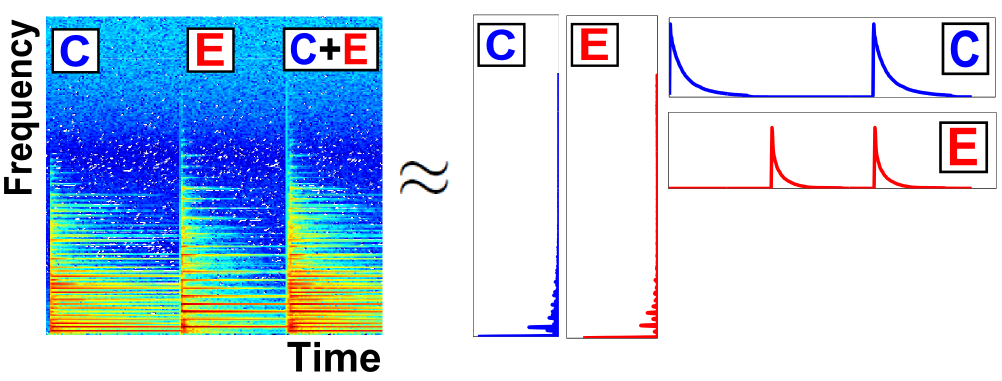左辺の行列は入力音楽 (の時間周波数情報) で，右辺の行列の積はNMFによる解析結果です．
右辺の縦長の行列と横長の行列が，それぞれ「頻出パターン」と「頻出パターンがいつ現れるか」という情報にあたります．
NMFでやることは，左辺の「複雑な行列」を，右辺のような「直感的に意味が分かる行列」の積で表現することです．
右辺を見ることで，各音がどんな音色で，それぞれがいつ鳴るか，ということが分かります．
ただ，NMFには重大な問題点があります．
それは，データに含まれる頻出パターンの数が既知でなければいけない，ということです．
つまり，上の例でいえば，NMFを実行する前に，頻出パターン数は2だと知っておく必要があるということです．
誤った数を設定してしまうと，解析結果が深刻に劣化します．
具体的にいうと，小さすぎる値 (例えば1) の場合にはドとミの混合音を1つの音と見なしてしまったりし，
大きすぎる値 (例えば3) の場合にはドという1つの音を無理やり分けて2つの音と見なし
てしまったりします．
市販の音楽を構成する音の数は未知で，それを正確に推定することも困難です．
そこで，本研究室では，頻出パターン数が未知のもとでもNMFを実行できる手法を
提案しています．
下図は，上と同じ入力音楽に対して提案法を適用したときの図です．
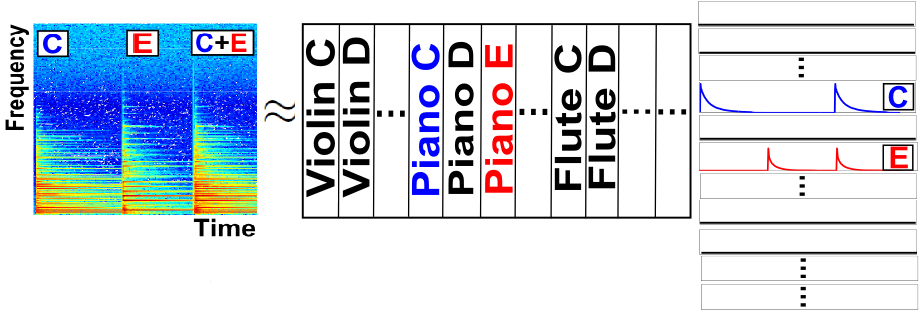提案法では，頻出パターン (楽器音) をあらかじめ用意しています．
このようにすることで，混合音を1つの音と見なしてしまったり，1つの音を混合音と見なしてしまったりすることがなくなります．
もちろん，同じ「ピアノのド」でも，メーカーや録音環境によって音色は異なりますが，提案法ではその差は無視できる程度であると仮定
しています．
入力音楽には使われていない楽器音まで用意していますが，それらの音は「音量が0の状態で鳴っている」と考えれば問題ありません．
提案法でやることは，入力音楽で使われている楽器と音高を判断し，その各音がいつ鳴っているかを求めることです．
当研究室では，最新の凸最適化理論に基づいてその問題に取り組んでいます．
研究テーマD
Sparse Adaptive Filtering Algorithm
担当：外田脩，田原勇太
適応フィルタ（Adaptive Filter）とは，未知のシステムの入出力関係から未知系の特性を推定する技術です．その概要については適応信号処理と非線形への拡張で説明されているので，ここでは，具体例とともに本研究室の最近の研究を紹介します．
・エコーキャンセラ
電話で通話していると自分の話した声が電話を通して帰って来た経験がある人は多いと思います．これらを防ぐために，現在の電話ではエコーキャンセラという信号処理技術が使われています．
エコーが発生する原因は，［自分の音声］が相手側のスピーカから出力される際に，相手側の入力マイクに再び入力されることにあります．
結果として，入力マイクに入力された［相手の音声（所望信号）］と［自分の音声（エコー成分）］が混ざった音が，自分側のスピーカから返されてしまいます．
この［エコー成分］を取り除き，［所望信号］のみを取り出す適応フィルタが必要になります．
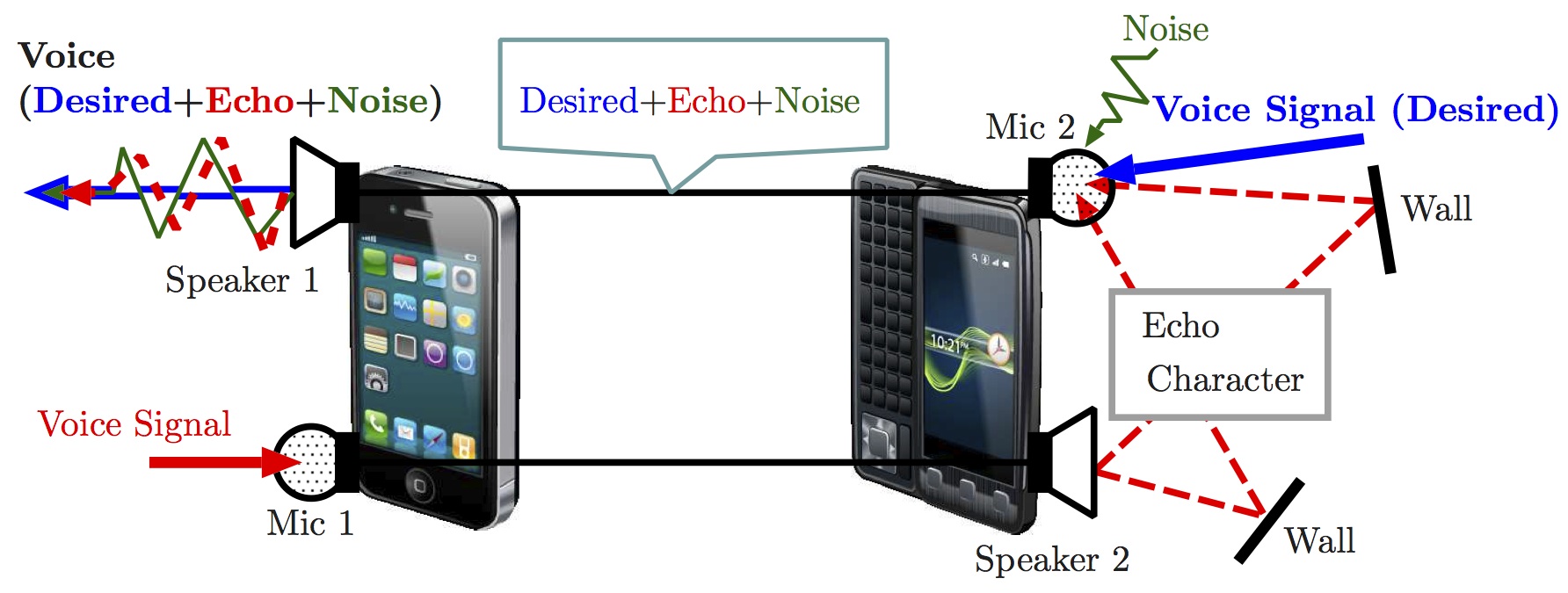
しかし，単純に音声を引けば良いわけではありません．スピーカから出力された音は直接マイクに届く音だけでなく，壁などに反響してマイクに届く音などがあるため，何らかの対処が必要となります．
そこで適応フィルタにより，スピーカから出力された音とマイクに入力された音（自分の音声＋相手の音声+雑音）から，スピーカからマイクまでの伝搬特性を推定します．
伝搬特性を把握することで，初めてエコー成分を正確に除去することができます．
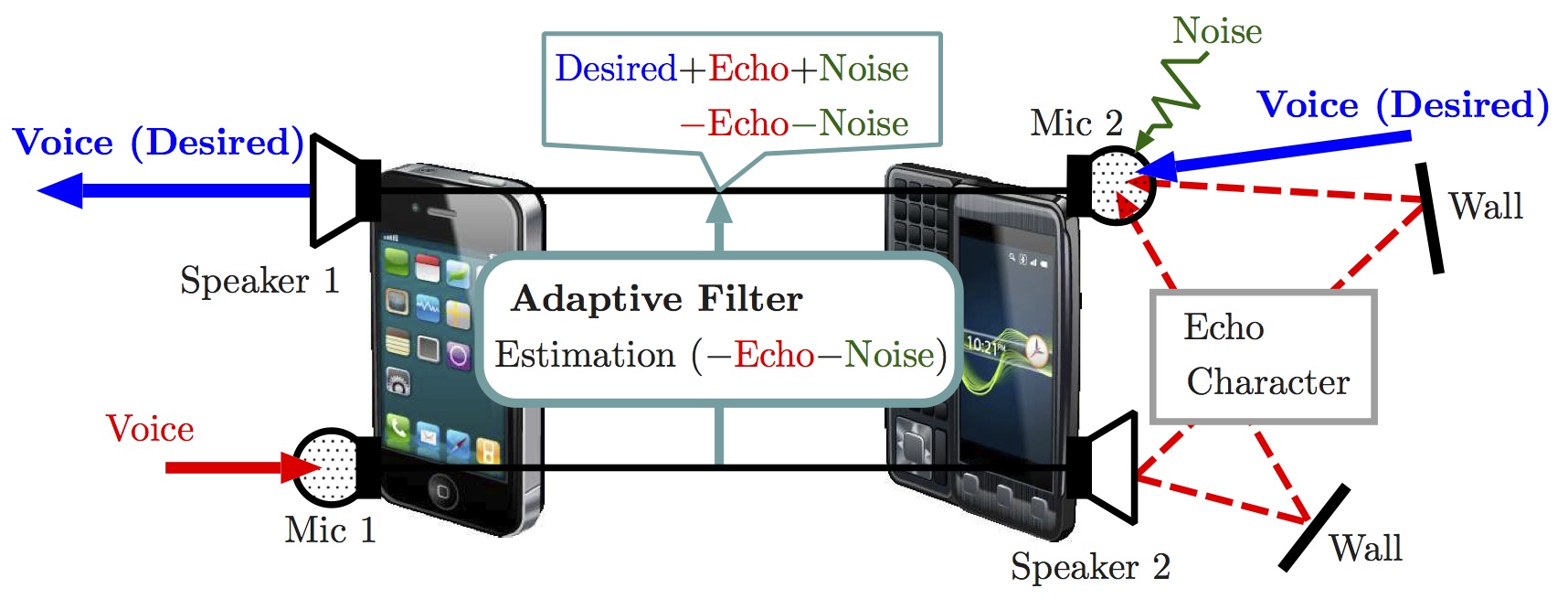
・等化器
無線通信において，送信側と受信側は離れた場所にあるため，送信信号をそのまま受信側に届けるのは非常に難しいです．
そのため，等化器によって受信信号から送信信号を復元することが必要となります．
等化器の基盤技術である適応フィルタは，伝送路の逆特性を推定することで，受信信号から送信信号を復元します．
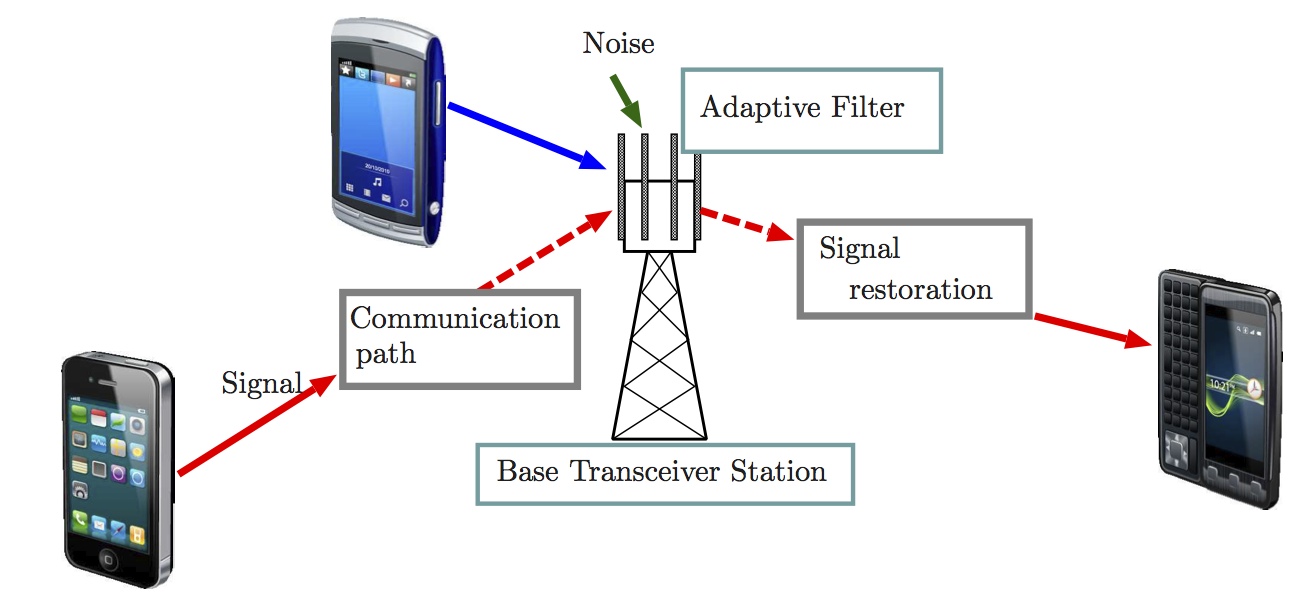
以上，音響・通信システムを御紹介しましたが，他にも様々な応用があります．
このように幅広い応用のある適応フィルタですが，本研究室では，「スパース(Sparse)」という性質に着目し研究を進めています．
スパースとは『疎（まばら）』という意味で、信号の多くが０、という性質です．
これまでの先行研究により，適応フィルタの多くの応用において未知系がスパースであること報告されています．
本研究室では，凸解析における最新の知見によってスパース性を効果的に利用する適応信号処理アルゴリズムの構築を目指して研究しています．
①スパース化
L1最小化はスパース性の促進に有効であることが知られています．
さらに，L1ノルムは凸性という優れた性質を有しており，この性質を適応アルゴリズムに反映することが，性能向上を実現することができます．
APFBS（Adaptive Proximal Forward-Backward Splitting）というアルゴリズムを応用した新手法を研究しています。
②計量射影法
一般的に「計量」は，距離を計る尺度のことと知られています．
例えば"東京と横浜を結ぶ"距離といっても
- 地図上の直線距離
- 地球曲面のゆがみを考慮した距離
- 実際の道路によって掛かる距離
など，様々なものがあります．
適切な距離を定義することで，効果的な推定ができることを実証しました．
最近の研究成果は「Asilomar2013；11月アメリカ」「ISWCS2013；8月ドイツ」などで発表予定です．