外れ値にロバストな信号復元法
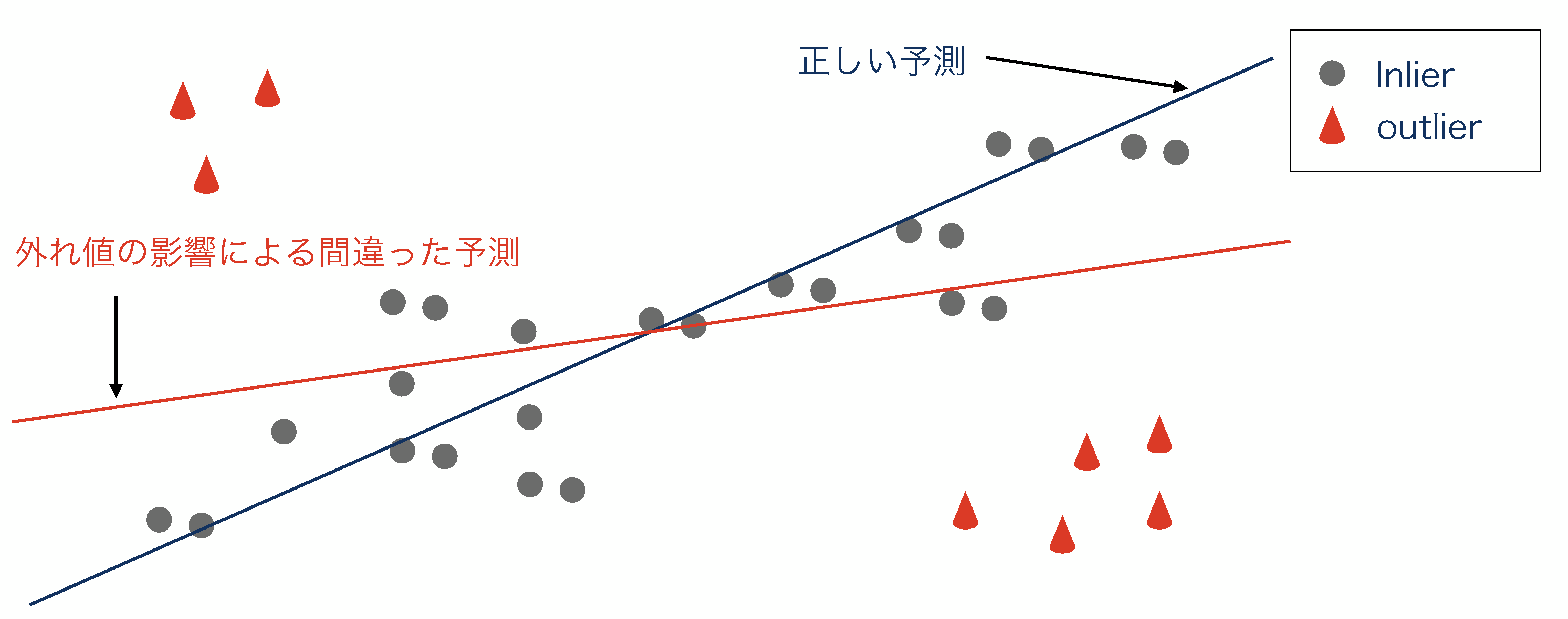
信号データ解析では、センサーの誤作動・入力ミス・突発性ノイズなど、様々な理由で全体の傾向から大きく外れたデータが混在することがよくあります。このようなデータは外れ値(outlier)と呼ばれ、間違った解析結果を招く要因となります(上図参照)。外れ値の影響を受けずらい「ロバスト統計」の研究が長年、行われてきましたが、これまでに提案されてきた主な統計手法には、「外れ値に対するロバスト性」と「数学的な扱いやすさ(収束保証)」の間にトレードオフがありました。
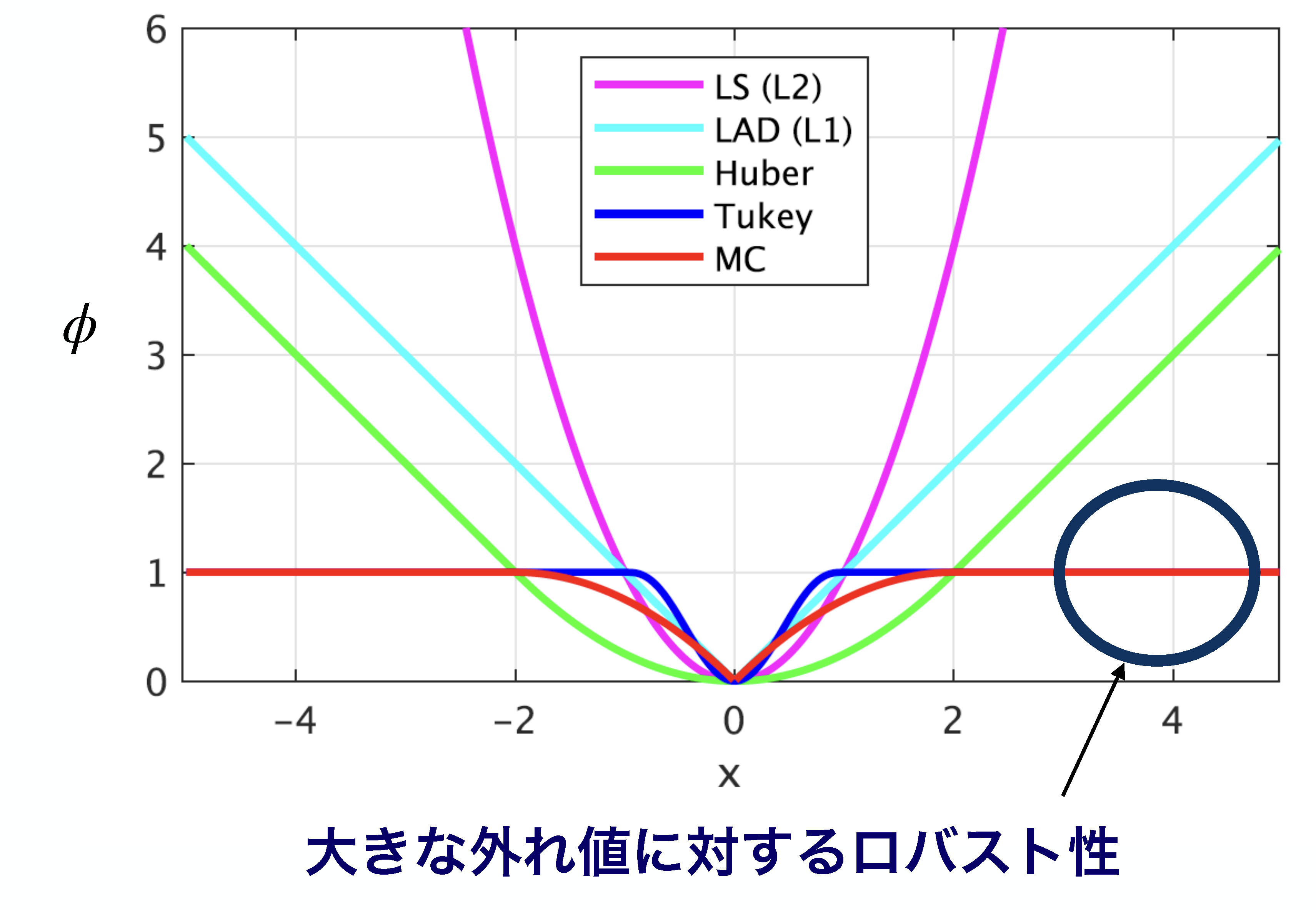
本研究では、「Moreau包に基づく正則化関数の機能強化」により、このトレードオフを解消し、既存のロバスト手法が劣化してしまうような大きな外れ値に対しても頑健なアプローチを提案しました。上図は、L1正則化関数をMoreau包で機能強化したMinimax Concave (MC) 関数を表ています。MC関数は、xが0から増えていくと、傾きが減っていき、最後は飽和して微分(勾配)がゼロになります。このMC関数を損失関数に用いることで、大きな外れ値の影響がゼロになってロバストな推定ができます。
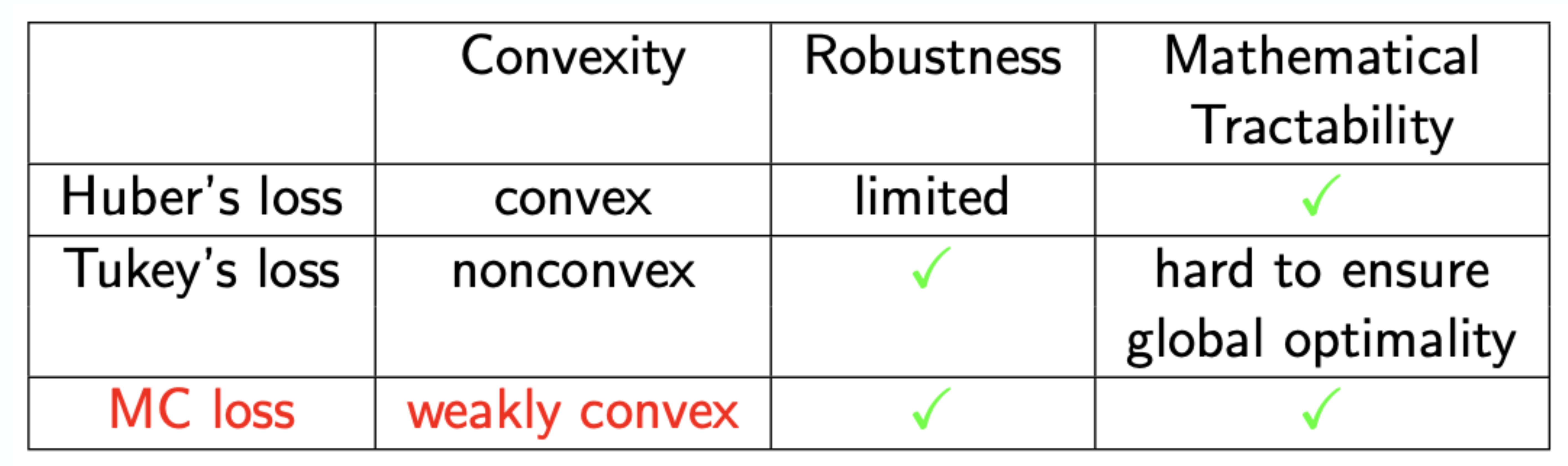
(本研究の一つのポイント) MC損失関数が「弱凸性」と呼ばれる「良質な非凸性(非線形性)」を持つおかげで、「外れ値に対するロバスト性」と「数学的な扱いやすさ(収束保証)」のトレードオフをうまく解消している点です。
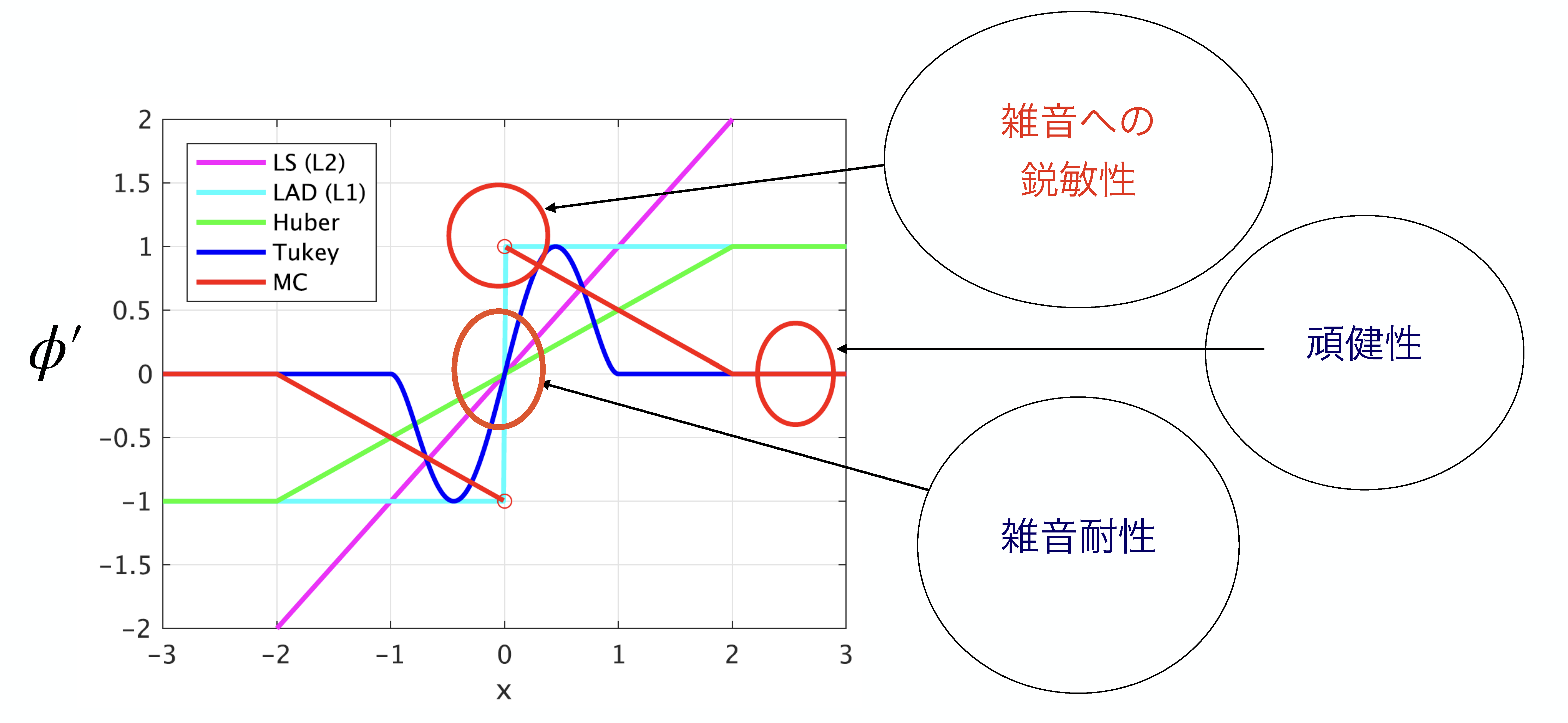
しかし、損失関数の微分を見てみると、潜在的な問題点が浮かんできます。上図の原点付近に着目してみましょう。Huber損失やTukey損失は、原点で微分が消失していることが分かります。これは、損失関数が微小なノイズの影響を受けにくいことを意味しています。MC損失関数は、原点で微分できませんが、原点付近の微分の極限が1になって、消失しないことが分かります。このことから、ノイズレベル(ガウス性雑音)が大きいときに、不安定な挙動を示す可能性が示唆されます。

そこで、上のような新しい定式化を提案しました。
(この定式化のポイント)補助変数ベクトルを導入することによって、
雑音を陽にモデル化している点です。
(もう少しだけ細かい説明) 雑音ベクトルのガウス性を補助変数のL2ノルムの2乗によって表現し、外れ値のスパース性(全体のデータに対する外れ値の割合が小さいと仮定)をMC関数によって表現した定式化になっています。(ついでに、求めたい信号(未知の係数ベクトル)もガウス分布から生成されていると仮定されています。)
この手法を、Stable Outlier Robust Regression (SORR)と呼びます。Stableは、ざっくり言えば、ノイズレベルの変化に対して、性能が急激に変化しないという性質を意味しています。
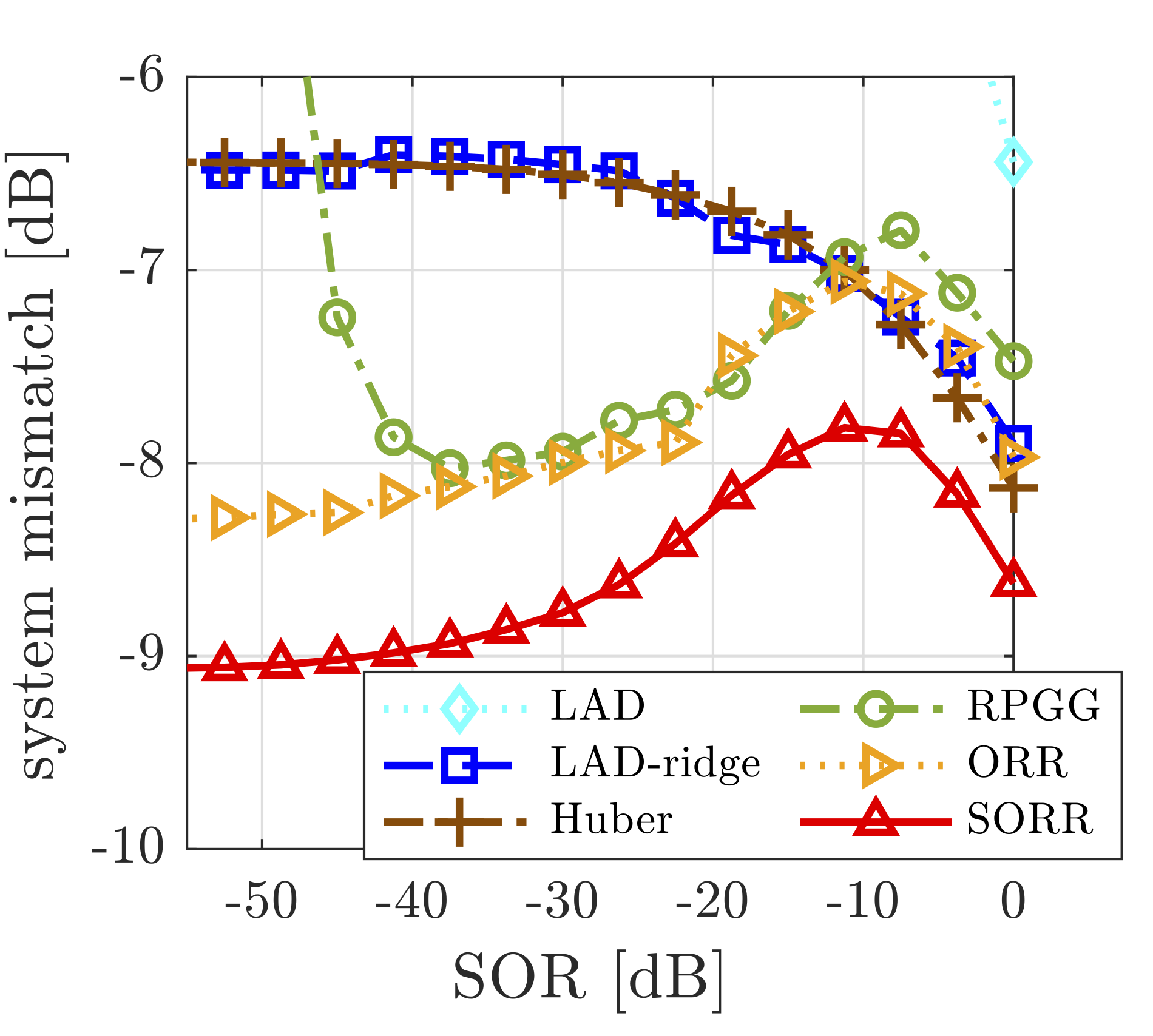
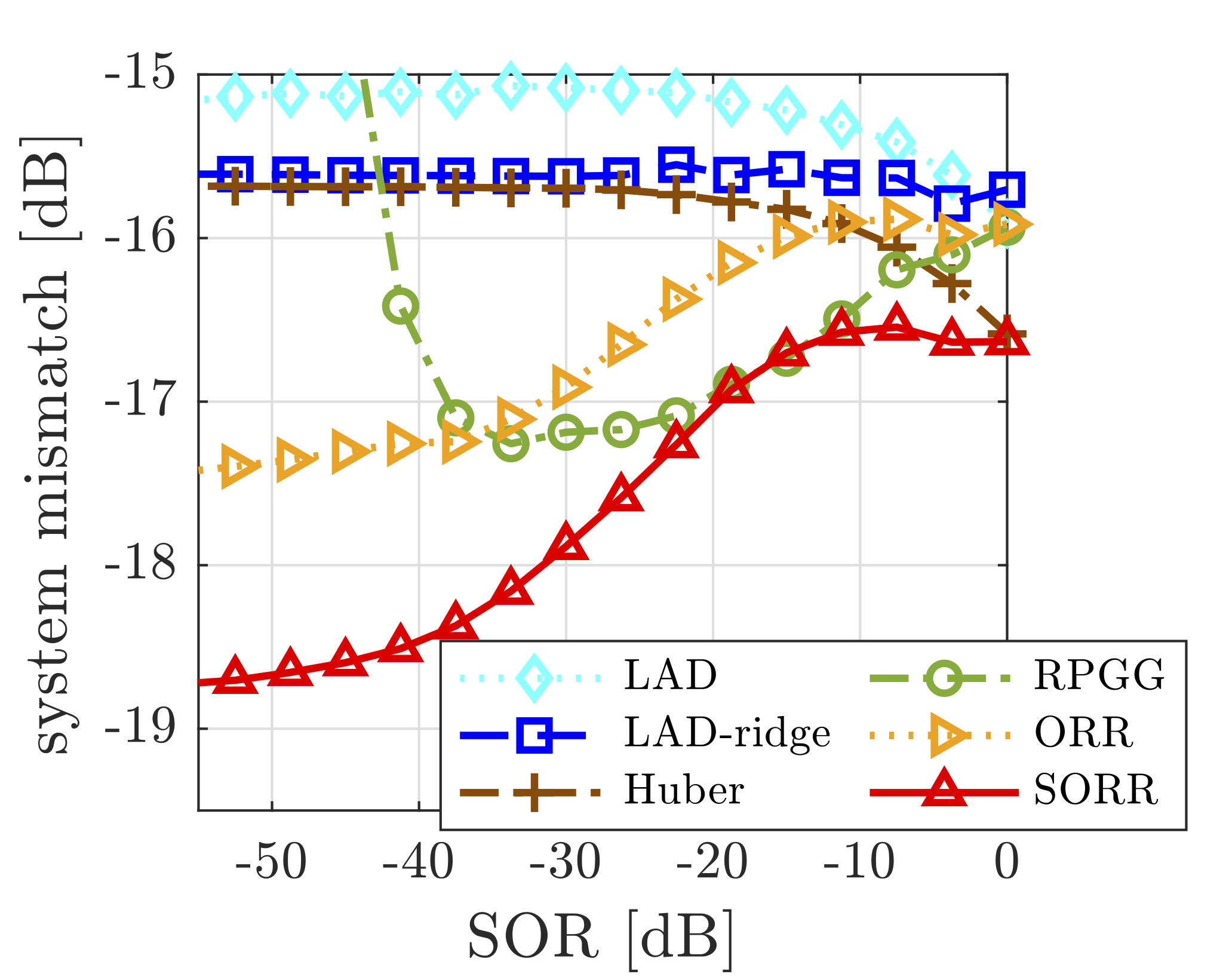
上図は、SNR 10 [dB], 外れ値の割合15%(上)とSNR 20[dB], 外れ値の割合10%(下)の時の結果です(Yukawa et al., IEEE Trans. Signal Processing,2023より抜粋)。横軸のSORは、信号と外れ値のパワーの比を表ていて、この値が小さいほど、外れ値のパワーが相対的に大きいことを意味します。
(示されたこと)ノイズレベルが高い場合でも、SORR(提案法)によって、大きな外れ値にロバストな推定が実現されました。
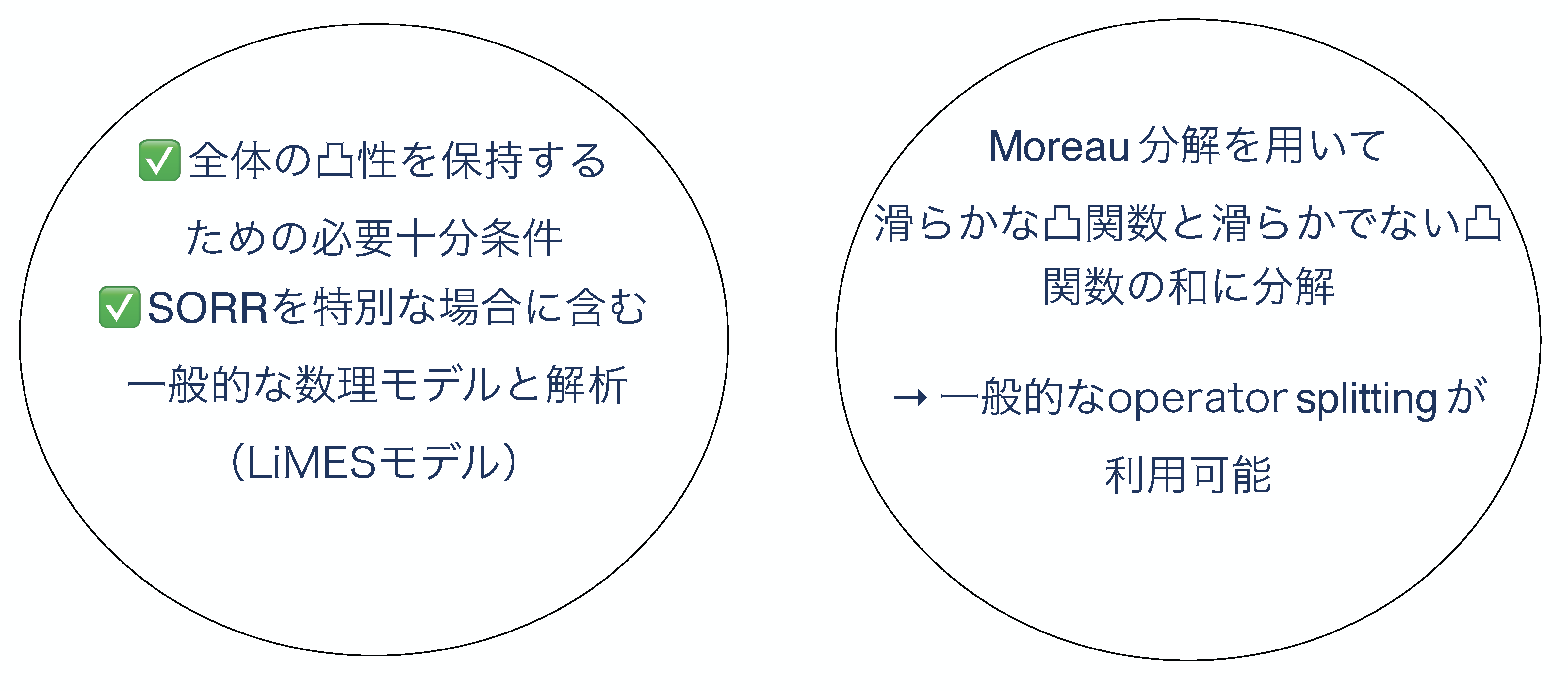
Yukawa et al., IEEE Trans. Signal Processing, 2023では、より一般的なLiMESモデルを提案しています。
上図は、本研究のポイントをまとめたものです。
研究プロジェクト
1. 外れ値に頑健なクラス識別器:ソフトマージンSVMとハードマージ
ンSVMをつなぐロバスト分類手法
Ryotaro Kadowaki and Masahiro Yukawa, ``LiMES-SVM: A robust classification approach bridging soft-margin and hard-margin SVMs,'' submitted. in Proceedings of IEEE MLSP, pp.1--6, London: UK, September 2024.
2. ネットワーク上のロバスト信号復元法:外れ値に頑健で、ガウス性雑音環境下でも安定な手法の提案
Maximilian Henri Vincent Tillmann and Masahiro Yukawa, ``Stable Outlier-Robust Signal Recovery Over Networks: A Convex Analytic Approach Using Minimax Concave Loss,'' IEEE Trans. Signal and Information Processing over Networks, vol.10, pp.690--705, 2024.
3. スパースモデリングのバイアス低減とロバスト推定のための一般的枠組みの研究:LiMESモデル
Masahiro Yukawa, Hiroyuki Kaneko, Kyohei Suzuki, Isao Yamada, ``Linearly-involved Moreau-Enhanced-over-Subspace Model: Debiased Sparse Modeling and Stable Outlier-Robust Regression'' IEEE Trans. Signal Processing, vol.71, pp.1232--1247, 2023.
4. 外れ値に頑健で、ガウス性雑音環境下でも安定な信号復元法
Kyohei Suzuki and Masahiro Yukawa, ``Sparse Stable Outlier-Robust Signal Recovery Under Gaussian Noise,'' IEEE Trans. Signal Processing, vol.71, pp.372--387, 2023.
5. 同時スパース性を持つ信号のロバスト復元法
Kyohei Suzuki and Masahiro Yukawa, ``Robust recovery of jointly-sparse signals using minimax concave loss function," IEEE Trans. Signal Processing, vol.69, pp.669--681, 2021.
